Мачурина Татьяна Николаевна,

г. Москва,

ГБУЗ Морозовская детская городская клиническая больница Департамента здравоохранения города Москвы,

клинический психолог, 

tama86@yandex.ru.

 

ТЕОРИЯ ХАОСА И ФРАКТАЛЫ В ПСИХОТЕРАПИИ И КЛИНИКО-ПСИХОЛОГИЧЕСКОМ КОНСУЛЬТИРОВАНИИ

 

Аннотация. Данная статья посвящена рассмотрению возможности применения странных аттрактов системы Э. Лоренца и фракталов Б. Мандельброта в психологической теории и практике.

Ключевые слова: хаос, уравнение, странный аттрактор, теория, фрактал, свойства, динамическая система, нелинейная система, Лоренц, психология, психологическое консультирование, психотерапия.

 

Machurina Tatyana Nikolaevna,

Moscow city,

GBUZ Morozovskaya Children's City Clinical Hospital of the Department of Health of the City of Moscow,

clinical psychologist,

tama86@yandex.ru.

 

CHAOS THEORY AND FRACTALS IN PSYCHOTHERAPY AND CLINICAL AND PSYCHOLOGICAL COUNSELING

 

Abstract. This article is devoted to the consideration of the possibility of using strange attracts of the system of E. Lorentz and fractals of B. Mandelbrot in psychological theory and practice.

Key words: chaos, equation, strange attractor, theory, fractal, properties, dynamic system, nonlinear system, Lorentz, psychology, psychological counseling, psychotherapy.

 

 

Возможно ли управление хаосом? Прогнозирование беспорядочного движения элементов какой-либо динамической системы? Существует ли в хаотическом распределении элементов определённый порядок и закономерность? Что влияет на хаотичность динамики и влияет ли? Ответы на данные вопросы были даны в 1972 году профессором метеорологии из Массачусетского технологического института (MIT) Эдвардом Лоренцем, обнаружившим в нелинейной системе обыкновенных дифференциальных уравнений явление, которое впоследствии получило название странного аттрактора (от английского attract — «притягивать»). С формальной точки зрения, аттрактор можно определить как «такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени» [2]. Важнейшим свойством аттрактора является то, что он имеет фрактальный характер и не представим в виде поверхности или кривой.

В ходе продолжительных экспериментов и вычислений Лоренцем была отмечена важная закономерность: хаотической динамической системе присуща значительная зависимость от исходных, первоначальных данных [3]. Лоренц пришёл к этому открытию, вычисляя значения в течение продолжительного времени и обнаружив в середине счёта некоторую особенность решения, побудившую его повторить свои вычисления с этого момента. Вначале получаемые при повторном счёте значения имели минимальное расхождение с предыдущими значениями, однако, по мере продолжительности эксперимента, расхождение между старыми и новыми данными становились всё более очевидными, пока, наконец, не стало ясно, что новое решение отнюдь не напоминает старое. Полученное явление получило общеизвестное название — «эффект бабочки» (чему послужило интригующее название одной из статей Лоренца — «Предсказуемость: может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?», 1972 г.) [8].

Ключевые идеи, сформулированные Лоренцем, можно обобщить следующим образом:

1.         Пусть взмах крыла бабочки способен вызвать торнадо, тогда с равной вероятностью тот же взмах способен предотвратить его образование;

2.         Пусть один взмах крыла бабочки вызывает торнадо, тогда той же способностью обладают все предыдущие и последующие взмахи, равно, как и взмахи крыльев всех остальных бабочек;

3.         Пусть взмах крыла одной бабочки, равно как и всех остальных бабочек, способен вызвать стихийное бедствие, тогда на это способен и человек со своей активностью, воздействующей на окружающую среду;

4.         Пусть взмах крыла способен вызвать торнадо, тогда он может изменить его траекторию или вовсе остановить его.

Не трудно заметить, что в основе данных идей лежит обнаруженная Лоренцем существенная зависимость поведения динамической системы от изначальных условий: взмах крыла насекомого выступает здесь в качестве причины незначительного изменения условий исследуемой системы, приводящей, вместе с тем, к самым разнообразным последствиям.

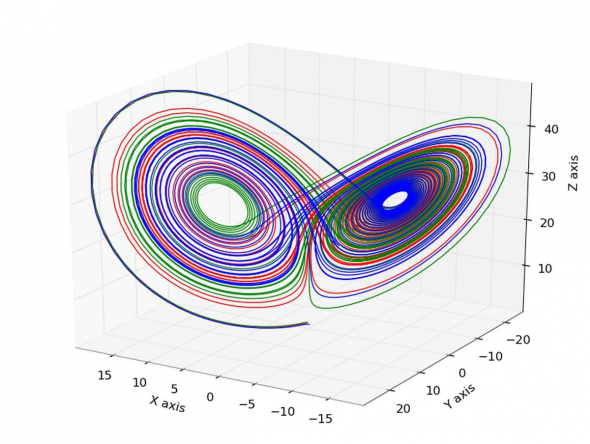
   Рис.1 Поведение траекторий в системе Лоренца

 

Значение теории хаоса в области психологических наук сложно переоценить. Понимание того, что хаос есть основа всего сущего, лишает научную психологию существующего в прежние времена устойчивого стремления привести личность к определённой, зависимой от конкретной психологической парадигмы, норме. Признаем, что личность — есть та самая хаотичная динамическая система с огромным количеством подвижных элементов, которая зависит, тем не менее, от неких начальных условий. Под начальными условиями, в данном случае, можно понимать как генетические особенности, так и раннее влияние окружающей среды (социальной, экономической, экологической). Но жизнь любого индивида — это постоянный хаос, состоящий из неисчислимого количества разнообразных явлений; возможно ли, в таком случае, длительное прогнозирование будущего, например, ребёнка раннего возраста, исходя из примерных начальных значений? Автору представляется разумным, что, исходя из теории Лоренца, подобные длительные прогнозы невозможны, либо могут носить исключительно вероятностный характер. А.Г. Шевцов пишет: «Сколь угодно малое воздействие может вызвать нелинейно-сильную реакцию и привести к структурному переходу системы. Спонтанная природа выбора дальнейшей траектории эволюции системы в точках бифуркации приводит к существованию спонтанности в микроструктуре развития личности» [5]. Вместе с тем, важно помнить, что, несмотря на кажущуюся беспорядочность (именно под этим понимается слово «хаос»), внутри динамической системы имеется непериодический порядок, благодаря чему внешне хаотичный набор элементов может быть упорядочен в разовые модели. Это даёт возможность, обладая знанием об определённых начальных данных, прогнозировать развитие личности в определённых пределах предсказуемости в ограниченном промежутке времени или периоде. Благодаря этому явлению в психологии были созданы, например, возрастные периодизации психического развития Л.С. Выготского, Д.Б. Эльконина, Ж. Пиаже, созданы определённые модели нормального и аномального развития.

Таким образом, хаос в теории Лоренца — это упорядоченный беспорядок, это динамическая система с непериодическими закономерностями. С. Манн, понимая, насколько понятие хаоса ассоциируется с представлениями о бесформенности и чистой случайности, предлагает своё определение — «нелинейная динамика». Манн подчёркивает, что теория хаоса не только не противоречит, но и происходит из классической физики и математики, но в то же время превосходит их, ведь классическая парадигма описывает линейное поведение объекта; дисциплина хаоса, напротив, рассматривает статистически и стратегически значимое поведение множества разнообразных взаимодействующих элементов.

В индивидуальной и семейной психотерапии, клинико-психологическом консультировании странные аттракторы находят своё применение в качестве рассмотрения пределов предсказуемости поведения личности (или целой семейной системы, или группы) как хаотичной динамики. Человеческий разум — нелинейная система, равновесие в которой — предельный случай [6]. Вместе с тем, можно заметить, что эта система при определённых условиях превращается в структуры аттракторов [6].

Рис.2 Система Лоренца

 

Хорошую иллюстрацию применения системы Лоренца дают Л.А. Паутова и А.К. Гуц [6]: если x – семейные отношения, y – отношения индивида с социальной средой (на работе, в школе, институте и т.д.), а z – это эмоциональное реагирование индивида, то справедливо, что состояние индивида в любой момент времени (t) характеризуется тремя переменными — x, y, z, отрицательное значение которых (-) означает способность индивида оказывать сопротивление негативным событиям в семье, социуме, контролировать своё психоэмоциональное состояние. Положительное значение трёх переменных (+), напротив, показывает неспособность решать проблемы, зависимость от своего негативного эмоционального состояния и т.д. Тогда первое уравнение в системе Лоренца демонстрирует скорость изменения отношений в семье, которые в большей степени зависят от качества социальных взаимоотношений (член qy) и способности индивида к регуляции семейных отношений (член -qx). Второе уравнение описывает скорость изменения социальных взаимоотношений: качество социальной деятельности находится в зависимости от семейных отношений (член rx) и его soft skills или социальных навыков (-y), а также переживаний индивидом семейных отношений (член -xz). Третье уравнение иллюстрирует скорость изменения психоэмоционального состояния человека (пассивность, реактивность и т. д.), которая в первую очередь определяется качеством социальных и семейных взаимоотношений (член xy), а также самоконтролем индивида (член -bz).

В психотерапии и клинико-психологическом консультировании речь клиента является хаотичной, нелинейной системой, вместе с тем содержащей тот самый непериодический порядок, присущий всем динамическим системам. Группы взаимодействующих элементов в данном случае можно рассматривать как кластеры, значимые смысловые единицы в устной речи клиента, представляющие для психотерапевта диагностическую значимость, позволяющие строить модель терапии, намечать её мишени и прогнозировать результаты.

      В психотерапии и клинико-психологическом консультировании нашла своё применение также теория фракталов (Б. Мандельброт). На языке математики фрактал — есть множество, обладающее свойством самоподобия. Иными словами, фрактал — есть целое, имеющее ту же форму, что и одна или более частей. Фракталы показывают себя во множестве самых различных объектов окружающего пространства, в их структуре, развитии и функционировании. От снежинки до человеческого мозга, фракталы неизменно являют себя человеческому взору.

 

Рис.3 Фракталы в природе

 

Что есть личностная установка, закреплённая поведенческая модель, личностная акцентуация, наконец? Повторяющееся дезадаптивное поведение в клинической картине невроза; обсессивно-компульсивное расстройство; патологические семейные паттерны, переходящие из поколения в поколение; поведение личности, отражающей поведение группы — всё это фракталы. В данном ключе психотерапия есть искусство создания рисунка личности клиента, в котором множество самых разнообразных элементов, согласно свойству самоподобия, постепенно складываются в единую логическую картину.

Обратимся к основным свойствам фракталов:

1.      Нерегулярность. Если описать фрактал функцией, то такая функция окажется не дифференцируемой, то есть, не гладкой ни в какой точке на всём своём протяжении. Применительно к психологии данный феномен можно проиллюстрировать аффективной лабильностью личности или циклотимией, которые как нельзя лучше демонстрируют эту нерегулярность или колебания. 

2.      Самоподобие. Данное свойство означает, что фрактал — это рекурсивная модель, каждый элемент которой в своём развитии повторяет развитие всей модели в целом. Примером в контексте данной статьи может служить психологическая теория рекапитуляции С. Холла, согласно которой главным законом развития является биогенетический «закон рекапитуляции», согласно которому индивидуальное развитие (онтогенез) повторяет главные стадии филогенеза. Иными словами, каждый ребёнок в своём индивидуальном развитии повторяет основные этапы развития всего человеческого рода.

3.      Размерность. Фрактальные объекты имеют топологическую размерность, характеризующую степень сложности кривой. Исследовав закономерности чередования разноразмерных участков и характер влияния на систему внешних и внутренних факторов, появляется возможность в определённой степени прогнозировать поведение системы. Относительно детской и семейной психологии это означает, что, к примеру, изучив «кривую» поведенческих реакции у ребёнка, а также влияющие на неё в данный период факторы, можно прогнозировать поведение всей семейной системы в целом. 

В настоящее время теория фрактального анализа в психотерапии всё чаще находит своих последователей. Автору представляется возможным использование данного метода в русле гештальт-терапии и системной семейной психотерапии.

Возможности использования теории хаоса и фракталов в психотерапии и клинико-психологическом консультировании обусловлены, в первую очередь, насущной потребностью психологических наук в развитии математических методов исследования, применимых для изучения личности и группы. Так, изучение психологических данных невозможно осуществить с помощью линейного, классического подхода. Поведение человека, сложные, противоречивые явления, происходящие в его психике не поддаются точному анализу и вычислению. В этом ключе странные аттракторы Лоренца, как и фракталы Мандельброта, прекрасно демонстрируют модель неклассического мышления с его сложностью, неопределённостью, нестандартностью и нелинейностью.

Таким образом, математические дисциплины хаоса и фракталов могут равно эффективно применяться в изучении психологических феноменов.

 

Библиографический список.

1.       Данилов Ю.А. Лекции по нелинейной динамике. Элементарное введение. – М.: КомКнига, 2006.

2.       Гринченко В.Т., Мацыпура В.Т., Снарский А.А. Введение в нелинейную динамику: Хаос и фракталы. – М.: Изд-во ЛКИ, 2007.

3.       Гукенхеймер Дж., Холмс Ф. Нелинейные колебания, динамические системы и бифуркации векторных полей. – Москва-Ижевск: Институт компьютерных исследований, 2002.

4.       Деменюк С. Л. Просто хаос. – СПб.: ООО «Страта», 2013.

5.       Шевцов А.Г. Некоторые аспекты психосинергетического моделирования личности. – http://philopsy.wallst.ru/konfer/psihosiner51t.html.

6.       Л.А. Паутова, А.К. Гуц Использование теории хаоса и странных аттракторов в исследованиях индивидуального и социального сознания / Математические структуры и моделирование. – 2004. – вып.13. – С.126–131.

7.       Математическое моделирование в психологии. – Красноярск, 2001.

8.       Lorenz E. Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas? 1972.

9.       Ghys E. The Lorenz Attractor, a Paradigm for Chaos. 2010.

10.     Knill O. The Lorenz System. 2005.

11.     Semenova E. Chaotic behavior of dynamical systems. 2014.